.png){kind=logo}
LIOR ALON
I'm an instructor at the math department at MIT, where I was previously a postdoctoral researcher hosted by David Jerison, as part of the Simons collaboration on localization of waves.
Between 2020-2022, I was a postdoc at IAS (Princeton), hosted by Peter Sarnak. I received my Ph.D. from the Technion in 2020, where I had the pleasure of being advised by Ram Band.
My research lies within mathematical physics, and intersects with various mathematical disciplines, including Fourier Analysis, Spectral Geometry, Graph Theory, Morse Theory, Real Algebraic Geometry, Dynamics, and Number Theory.
Here are some of my recent works:
-
Higher Dimensional Fourier Quasicrystals from Lee-Yang Varieties
joint with Kurasov, Kummer, and Vinzant -
Universality of nodal count distribution in large metric graphs
joint with Band and Berkolaiko -
Generic Laplace eigenfunctions on metric graphs
-
Morse theory for discrete magnetic operators and nodal count distribution for graphs
Joint with Goresky
A detailed list of publications is found below, as well as nice pictures from these works and other projects.
My contact - lioralon@mit.edu
Here is my CV and Research Statement
RESEARCH
PUBLICATIONS
Higher Dimensional Fourier Quasicrystals from Lee-Yang Varieties
L Alon, M Kummer, P Kurasov, C Vinzant
Accepted to Inventiones Mathematicae
Gap distributions of Fourier quasicrystals via Lee-Yang polynomials
L Alon, A Cohen, and C Vinzant (2024)
Revista Matemática Iberoamericana
Morse theory for discrete magnetic operators and nodal count distribution for graphs
L Alon, M Goresky (2024)
Journal of Spectral Theory
Every real-rooted exponential polynomial is the restriction of a Lee-Yang polynomial
L Alon, A Cohen, and C Vinzant (2023)
Journal of Functional Analysis
Generic Laplace eigenfunctions on metric graphs
L Alon (2023)
Journal d'Analyse Mathématique. doi: 10.1007/s11854-023-0308-x
Universality of nodal count distribution in large metric graphs
L Alon, R Band, G Berkolaiko (2022)
Experimental Mathematics
Neumann domains on quantum graphs
L Alon, R Band (2021)
Annals of Henri Poincare
Neumann domains on graphs and manifolds
L Alon, R Band, M Bersudsky, S Egger (2020)
Analysis and Geometry on Graphs and Manifolds
Nodal statistics on quantum graphs
L Alon, R Band, G Berkolaiko (2017)
Communications in Mathematical Physics
Cerenkov radiation from particles carrying orbital angular momentum in a cylindrical waveguide
Y Shapira, M Mutzafi, G Harari, I Kaminer, L Alon, M Segev (2016)
Conference on Lasers and Electro-Optics (CLEO)
PREPRINTS
Nodal count for a random signing of a graph with disjoint cycles
L Alon, M Goresky (2024)
arXiv preprint arXiv:2403.01033
Average Nodal Count and the Nodal Count Condition for Graphs
L Alon, J Urschel (2024)
PH.D. THESIS
Quantum graphs - Generic eigenfunctions and their nodal count and Neumann count statistics
L Alon
VIDEO
FOURIER QUASICRYSTALS
QUANTUM GRAPHS
This gif shows the evolution of a wave function on a quantum graph.
In this plot we see |f(x,t)|^2 (the probability density) changing in time according to Schrödinger's equation, starting from a Gaussian of positive velocity.
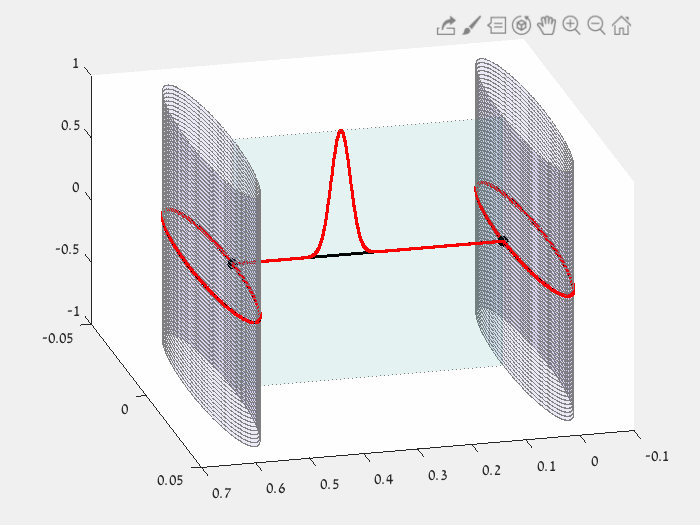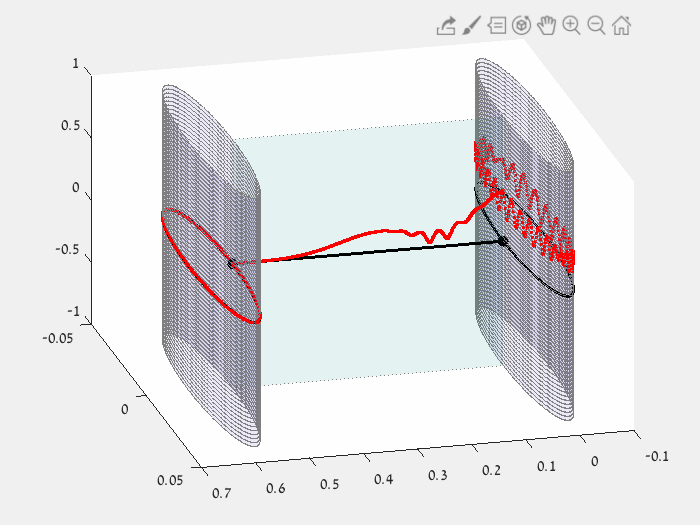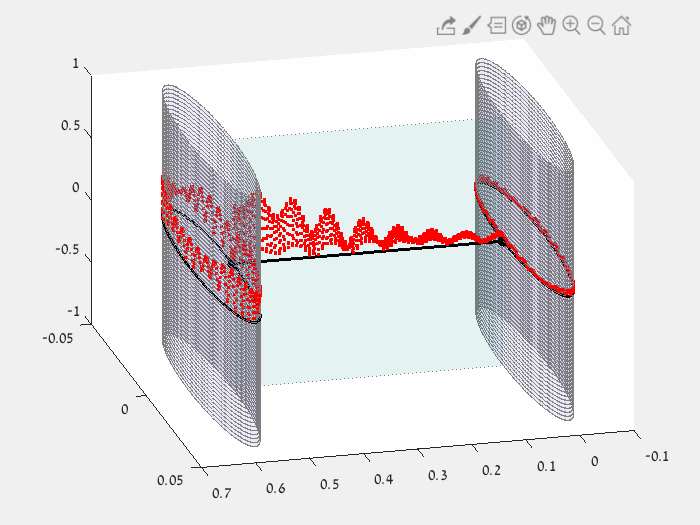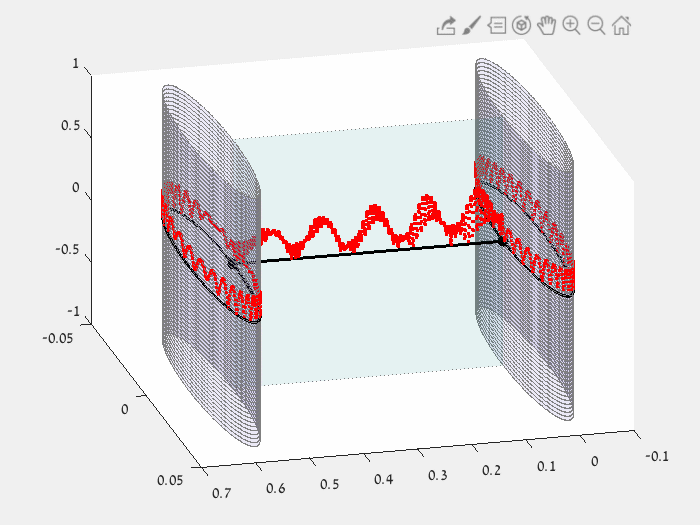
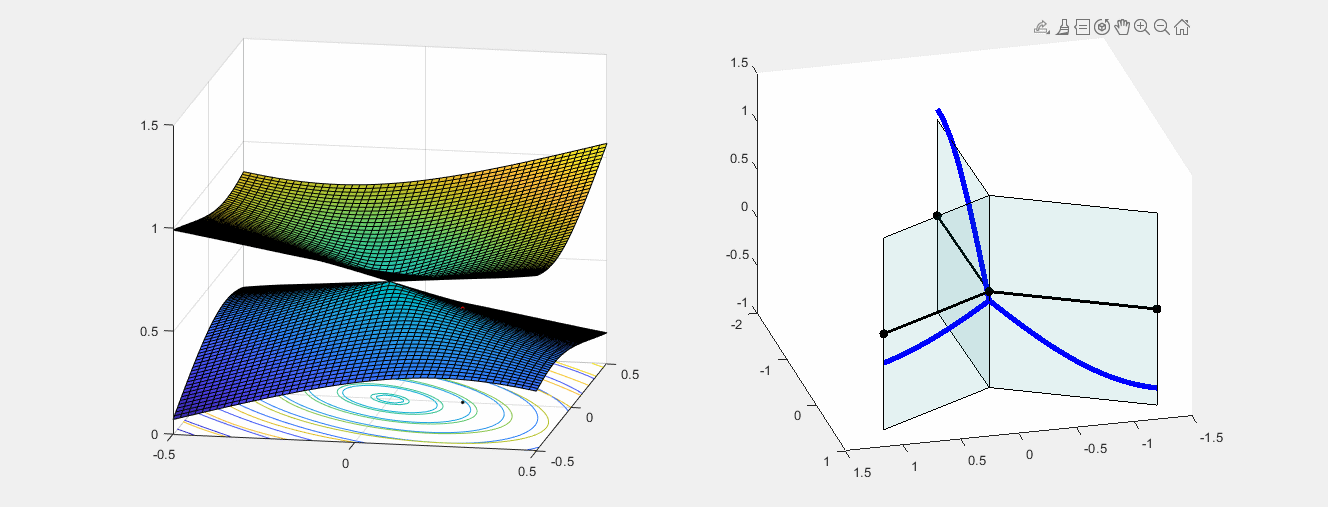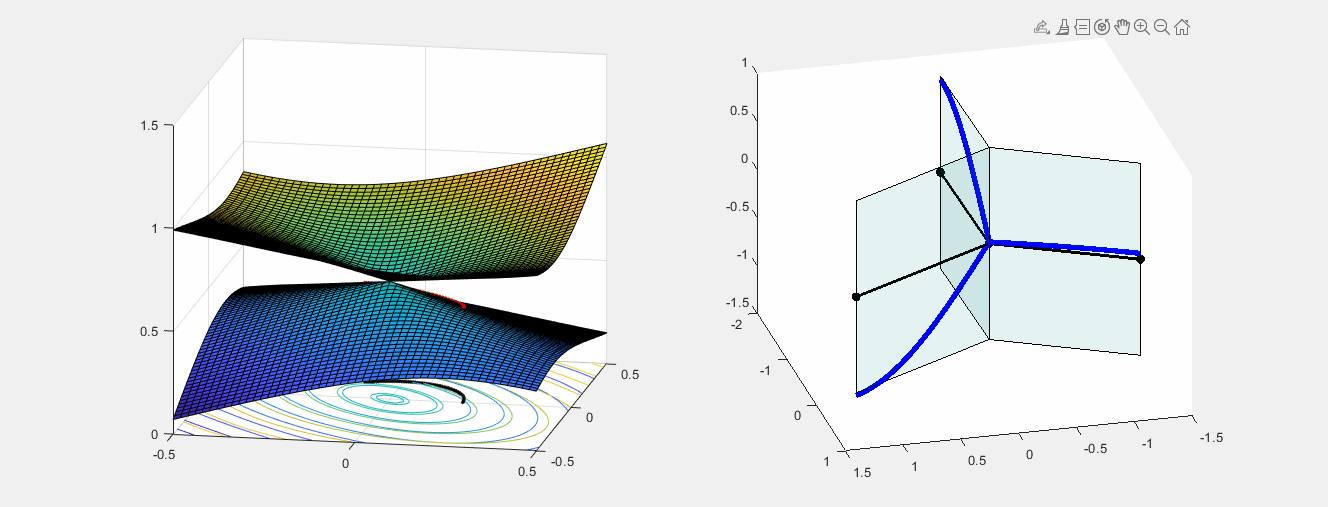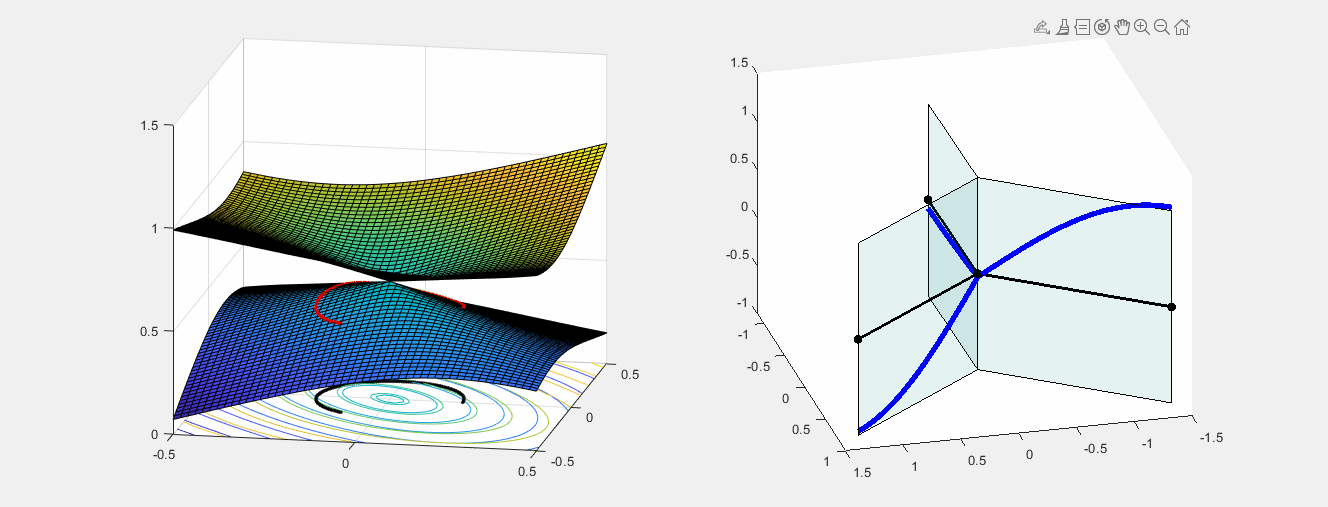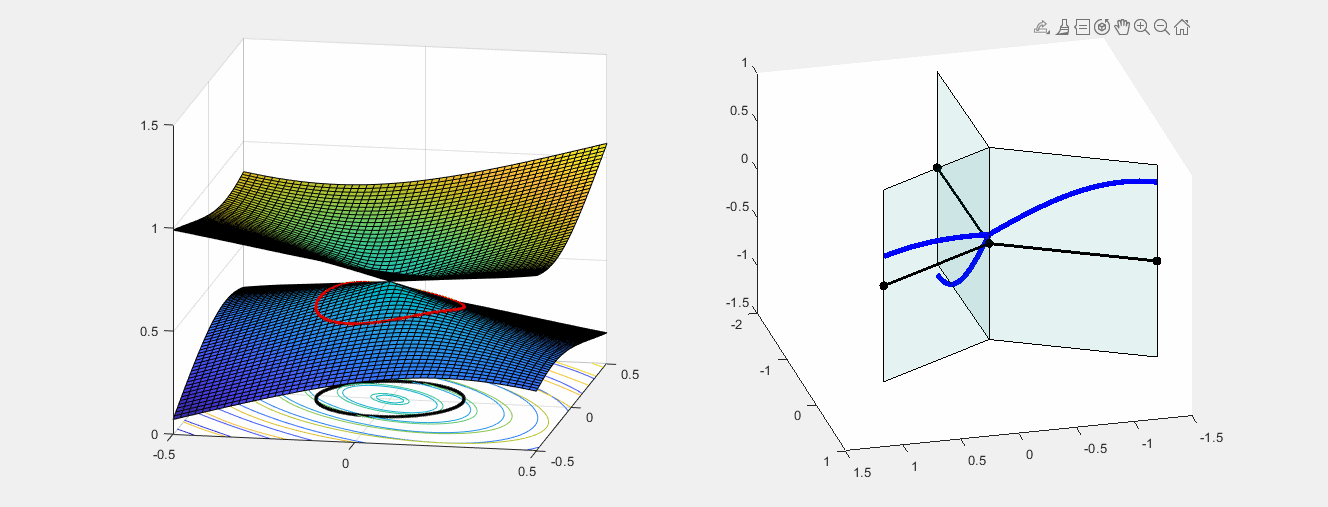
BERRY PHASE
How a continuous periodic change of edge lengths can "flip" an eigenfunction.
Left: closed path in the parameter space - possible edge lengths (L1,L2,L3) for which the star graph has eigenvalue equal to 1.
Right: The corresponding eigenfunction of eigenvalue 1, changing continuously with the edge lengths.
RELATED IMAGES
By clicking on each image you can see its description and a link to the relevant poster
 |  |  |
|---|
CONTACT
MIT- Massachusetts Institute of Technology
77 Massachusetts Ave, Cambridge, MA 02139-4307
USA
Mathematics department, Room 241
Home Address: 1 Dana street, apartment 20, Cambridge, MA 02138
Email: lioralon@mit.edu
Secondary Email: